Click here for an Acrobat version of this document.
Orbital mechanics deals with describing and predicting the position, velocity and centripetal acceleration on a body that is being orbited by a satellite. (A satellite is anything -space shuttle, sputnik, astronaut, moon, ring of moonlets, communications satellite- that orbits another object.) In all cases gravity supplies the centripetal force.
Gravity's pull is described by Newton's "Law of Universal Gravity." Mathematically this is described as.

Because of Newton's third law of motion, for every action there is an equal and opposite reaction, the force m1 exerts on m2 is equal to the force m2 exerts on m1. If "m1" pulls on "m2" with a force of 20 000 N then "m2" pulls on "m1" with a force of 20 000.
The distance between to objects or planets is measured between their center of masses.
Some Solar system data (Do not memorize. You will always have access to this information.)
G = 6.67259 x 10-11 (N•m2)/kg2
Earth
Mass 5.98 X 1024 kg
Radius 6.38 X 106 m
Mean distance from the Sun 1.50 X 1011 m
Sun
Mass 1.99 X 1030 kg
Radius 6.96 X 108 m
Moon
Mass 7.35 X 1022 kg
Radius 1.74 X 106 m
Mean distance from the Earth 3.85 X 108 m
EXAMPLE 1
What is a the pull of gravity on a person on the surface of the Earth it the person's mass is 55.5 kg?
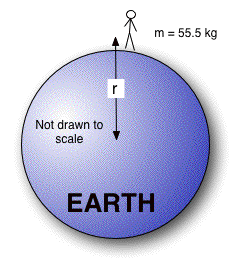
Givens |
Unknown |
Strategy |
From the table
G = 6.67 x 10 -11 (N·m 2 )/(kg 2 )
r= 6.38 X 10 6 m (radius of the Earth)
m EARTH = 5.98 x 10 24 kg |
Gravity's Pull is "F" in the universal gravity formula |
• Since the question asks for the pull of gravity, use the universal gravity formula.
• Get givens from the solar system data table.
• Because the person is on the surface of the Earth, use the Earth's radius as the distance.
• The two masses are the Earth's from the table and the person's.
• Plug and chug out the answer. |
Formula and math |

|
Note: w=mg. This means that (55.5 kg)(9.8 m/s 2 ) = 543 N. It is the same answer as above.
Universal Gravity and Orbital Mechanics
We will mathematically address perfectly circular orbits -for now. Because the object's travel in a circle, they feel a centripetal force. This centripetal force is supplied by Gravity. Recall in class we discussed that the centripetal force must be supplied by something. This "something" is gravity for orbiting satellites.
Gravity's pull = Centripetal force
Therefore, this means the following mathematically

Since "m2" in the centripetal force equation is the mass of the satellite and m2 in the universal gravity formula is also for the satellite, they will cancel each other out. This leaves the following formulae.

Remember, "m1" is the mass of the object being orbited.
Note : Come test time, you will be given the circular motion formulae but NOT the formula for universal gravity . Memorize it !!!
Problem solving strategy:
Use these relationships when you are given a question involving objects that orbit each other. (Later we will add one more technique for this style problem with a unique set of givens.)
- List the givens. Remember whenever the Sun, moon or Earth are mentioned in a problem, use whatever values are necessary in the information table.
- Set the centripetal force equal to the gravitational force.
- Choose one of the 3 centripetal force formulae by looking at your givens and unknown. Use algebra to isolate the unknown.
Example 2
What is the period of motion for Earth's moon?
Givens |
Unknown |
Strategy |
From the table
G = 6.67 x 10 -11 (N·m 2 )/(kg 2 )
r= 3.85 x 10 8 m
m EARTH = 5.98 x 10 24 kg |
Period => T |
• Set the centripetal force equal to the universal gravity.
• Get givens from the solar system data table.
• For the centripetal acceleration formula, use the one with "r" and "T" in it.
• Use algebra to solve for T. |
Formula and math |

|
Example 3
What is the velocity of the Earth as it travels around the Sun?
Givens |
Unknown |
Strategy |
From the table
G = 6.67 x 10 -11 (N·m 2 )/(kg 2 )
r= 6.96 X 10 8 m
m SUN = 1.99 X 10 30 kg |
Velocity = v t |
• Set the centripetal force equal to the universal gravity
• Get givens from the solar system data table.
• For the centripetal acceleration formula, use the one with "r" and "v t " in it.
• Use algebra to solve for v t . |
Formula and math |

|
Kepler's 3 Laws of Planetary Motion
Law #1
All orbits are elliptical in shape. If a planet orbits in a circular path, it still obeys the law. A circle is a special case of an ellipse where the 2 foci are at the same location. This law does not imply that some massive object need to be at each foci. It only need to be at one of the foci.
Law #2
A quantity called angular momentum must be conserved for the satellite orbiting the planet. Usually this is stated as equal areas between the body being orbited and the satellite in equal time intervals are equal. The picture bellow shoes a planet orbiting a star. The each line is a radius between the sun and planet. Each line was drawn at the first of the month. The law says that the areas between the lines are equal because they were drawn at equal intervals in time.

Law #3

Finding Kepler's constant is very valuable in solving problems. However, using this law a ratio is very valuable. When solving problems using Newton's Law of Universal gravity and orbits, you almost always needed the mass of the body being orbited. Using the 3 rd Law of Planetary Motion gets around needing to know the body's mass.
EXAMPLE 4
A geosynchronous orbit occurs when a satellite orbits with the same period of motion as the object being orbited. The planet Mars spins around on it axis once every 24 hrs and 29 minutes. One of Mars's moons, Phobos, orbits closer to the surface than any other moon in the solar system. Its orbit is 9378 km from the center of Mars. Its period of motion is 4.32 hours. If we are to put a station in geosynchronous orbit above Mars, how high should the orbit be above the surface of Mars it Mars's radius is 3 397 000 m?
Givens |
Unknown |
Strategy |
r= 9378 km (Phobos)
T=4.32 hrs (Phobos)
T=24 hrs & 29 minutes (Mars) |
Period => T for the station |
• Because no masses are given in the table or in the problem, Kepler's 3 rd Law of Planetary Motion will have to be used.
• Units do not need to be in the SI system to use the 3 rd Law of Planetary Motion. They only need to be the same.
• Set T2/r3 for Phobos equal to T2/r3/ for the station.
• Use the period of motion for Mars' rotation for the station because it is to be places in a geosynchronous orbit.
• Subtract the radius of Mars from the orbit to find the distance above the surface of the planet. |
Formula and math |

|
|