Getting the Coaster Started
(Work, Kinetic Energy, Potential Energy , Kinematics and Power)

Coaster Design Home Page

Getting The Coaster Started

Something has to be done to get the coaster started. In our previous example energy, power, has to added get the coaster up to 8.8 m/s. This is done by doing work on the coaster. A simplified definition of work would be force times displacement when the force and displacement go in the same direction. [This chapter will not go into all the details of calculating work.] Suffice it to say that when the force acting on the coaster and the displacement of the coaster are in the same direction, work adds energy to the coaster. When the force acting on the coaster and the displacement of the coaster are in opposite directions, work removes energy from the coaster.

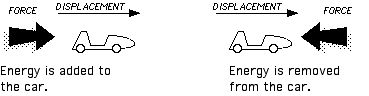
Work = (Force)(Displacement)
W = Fd
Where “work” is measured in joules, J. “Force” is measured in Newtons, N, and “displacement” is measured in meters, m.

Example 3
What is the velocity of the train after being catapulted into motion?


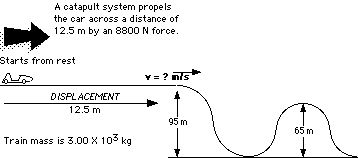
Solution:
ET_{(BEGINNING) + Work} = ET_{(TOP OF THE 1}^st _HILL)
KE + PE +W = KE +PE
(¹/2)mv² + mgh + Fd = (¹/2)mv² + mgh
(¹/2)3000(0)² + 3000(9.8)(0) + 8800(12.5)= (¹/2)3000v² + 3000(9.8)(0) Substitute the numbers at each
location
110,000 = (¹/2)(3000)v²
73.333 = v²
v = 8.56 ^m/s ... at the end of the catapult.
As an aside you can calculate the acceleration of the rider from kinematics equations.
(For the curious the acceleration is 7.0 ^m/s²)


Example 4
What is the velocity of the train after being hauled up a hill by chain driven motor system?

^`
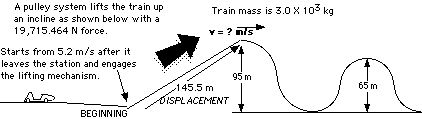
Solution:
ET_{(BEGINNING) + Work} = ET_{(TOP OF 1}^st _HILL)
KE + PE +W = KE +PE
(¹/2)mv² + mgh + Fd = (¹/2)mv² + mgh
(¹/2)3000(5.2)² + 3000(9.8)(0) + 19,715.464(145.5) = (¹/2)3000v² + 3000(9.8)(95)
40560 + 2868600.012 = (¹/2)(3000)v² + 2793000
116160.012 = (¹/2)(3000)v²
77.44 = v²
v = 8.8 ^m/s at the top of the hill


Example 5

A roller coaster train of mass 3.0 X 10³ kg rolls over a 11.5 m high hill at 8.34 ^m/s before rolling down into the station. Once in the station, brakes are applied to the train to slow it down to 1.00 ^m/s in 5.44 m.

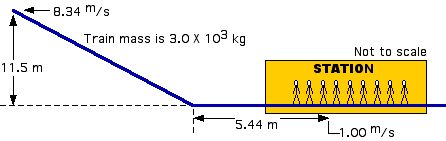
(a) What braking force slowed the train down?
(b) How much time did it take to slow the train down?
(c) What was the acceleration of the train in g’s?

Solution:
(a)
ET_(HILL) = ET_{(@ 1 m/s) + Work}
KE + PE = KE +PE +W
(¹/2)mv² + mgh = (¹/2)mv² + mgh + Fd
(¹/2)3000(8.34)² + 3000(9.8)(11.5) = (¹/2)3000(1)² + 3000(9.8)(0) + F(5.44) Substitute the numbers
at each location
442433.400 = 1500 + 5.44F
F = 81053.9 N ...force to slow down the train
(b)
Calculate the velocity as the train enters the station. Use this velocity to calculate the time.
ET_(HILL) = ET_{(@ STATION ENTRANCE)} No work is done because no force other than gravity acts between the two locations
KE + PE = KE +PE
(¹/2)mv² + mgh = (¹/2)mv² + mgh
(¹/2)3000(8.34)² + 3000(9.8)(11.5) = (¹/2)3000v² + 3000(9.8)(0) Substitute the numbers
at each location
442433.400 = 1500v²
v = 17.174
v = 17.2 ^m/s ...as the train enters the station.

The time is calculated from
v_o = 17.174 m/s
v_f = 1.00 m/s
x = 5.44 m
t = ?

t = 0.599 sec
(c)
Calculate the acceleration in ^m/s². Then convert it into g’s.
F= ma
81053.934 N = (3000 kg)a
a = 37.018 ^m/s²
a = 37.018 ^m/s²/ 9.80 ^m/s² = 3.78 g’s ... Yeow! That’s a big jerk on the passengers
into the restraining harness.